绝对星等 （absolute magnitude） $M$

设想把天体放在10秒差距(pc)(1pc=3.26光年)距离远的地方时所得到的视星等。

\begin{equation}
m-M=5\text{log}({d/10\text{pc}})
\end{equation}

视星等 （apparent magnitude） $m$

由视亮度或流量定义的星等称为视星等。

若两个天体在某个波段的流量分别为$f_{1}$和$f_{2}$，则两个天体的星等差异为：

\begin{equation}
m_{1}-m_{2}=-2.5\text{log}({f_{1}/f_{2}})
\end{equation}

若$f_{2}$是星等定义为0的恒星流量，即该测光系统的零点，则$m_{1}$为天体的视星等。

Vega星等

定义所有波段Vega星等都为0

而不同波段Vega星的流量都不同，因此不同波段的零星等流量也是不同的。

AB星等

AB星等在V波段的流量定标与Vega相同

但是AB星等在任何波段的零等星流量均为3631Jy

\begin{equation}
1 \text{ Jy} = 10^{-26} \text{ W m}^{-2} \text{ Hz}^{-1}=1 \times 10^{-23} \text{ erg s}^{-1} \text{ cm}^{-2} \text{ Hz}^{-1}
\end{equation}

若某个天体流量密度为$f_{v}$，单位是$\text{ erg s}^{-1} \text{ cm}^{-2} \text{ Hz}^{-1}$，则其在AB星等下的星等为：

\begin{equation}
m_{AB}=-2.5\text{log}({f_{v}})-48.6
\end{equation}

将上述定义扩展至宽波段后，AB星等可以定义为：

\begin{equation}
m_{AB}=-2.5\text{log}(\frac{\int^{\infty}_{0}f_{v}(\lambda)S^{obs}(\lambda)\text{d}\lambda}{\int^{\infty}_{0}S^{obs}(\lambda)\text{d}\lambda})-48.6
\end{equation}

$S^{obs}$是观测通带的透过率，其包含了从地球大气、光学系统到仪器本身的响应。

巴耳末减幅（Balmer decrement measures）$ D，c_{1}$

热光度(bolometric luminosity)$L_{bol}$

①一颗恒星 (一个天体)对所有波长积分的总光度$L_{bol}$。
②其实，我们不能测量一颗星所有的光，即不能测得恒星的热光度。我们只能用恒星大气模型来求得有多少能量在我们不能直接观测的区域发射出来。

热星等（bolometric magnitude）$m_{bol}$和热改正（correction）BC

恒星的绝对热星等($M_{bol}$)：

\begin{equation}
M_{bol}=-2.5log_{10}L_{bol}+C_{bol}
\end{equation}

$C_{bol}$定义为恒星绝对热星等的标度零点。一般求恒星绝对热星等是通过光电目视绝对星等加上热改正：$M_{bol}=M_{V}＋BC$

一般定义$M_{bol}=0$时的光度为$3.055×10^{28}$W

热改正(BC−Bolometric Correction)：把恒星的目视星等换算成热星等必须加的改正值，定义为：

\begin{equation}
BC=M_{V}-M_{bol}
\end{equation}

热改正可以从实验得到或用理论方法计算。
注意：热改正BC只和光谱型有关，即如果两颗星有完全一样的光谱，它们就有完全一样的热改正，即使它们的光度不同。
不同光谱型的热改正可以查表

亮度（brightness）

色余（color excess）

天体的实测色指数与光谱型相同的天体的正常色指数之差。

天文学名词

若某天体观测在B波段和V波段观测到的星等差异为$B_{\text{obs}}-V_{\text{obs}}$，而真实（内禀）的颜色差异为$B_{\text{intrinsic}}-V_{\text{intrinsic}}$，则其色余为：

\begin{equation}
E_{BV}=(B_{\text{obs}}-V_{\text{obs}})-(B_{\text{intrinsic}}-V_{\text{intrinsic}})
\end{equation}

计算消光规律的色余方法

假设所挑选的消光探测源具有同样的内禀色指数，满足:

\begin{equation}
k_{x}=\frac{E_{rx}}{E_{cr}}=\frac{A_{r}-A_{x}}{A_{c}-A_{r}}
\end{equation}

其中，$x$是待测波段，$r$是参考波段，$c$是比较波段。$A$参见下文星际消光中的定义。

通过大量样本拟合$k_{x}$后，根据比较波段$A_{c}/A_{r}$可以得到待测波段的相对消光$A_{x}/A_{r}$。^[2]

Cardelli 等人发现，银河系从紫外到光学波段 (可扩展到近红外波段) 的消光规律可以用单参量 $R_{V} $来表示，其中 $R_{V}=A_{V}/E(B_V) $

[2].王钰溪, 高健, 姜碧沩, 等. 银河系和河外星系的消光规律及尘埃性质[J]. 天文学进展, 2018, 36(3): 283-305.

色指数（color index）$C$ or $CI$

用不同测光系统近同时测得的同一天体的星等差。可以反映天体的颜色。

https://nadc.china-vo.org/astrodict/termdetails?id=6776

一个天体两个滤光片的星等之差称为颜色，也称为色指数：如$m_{B}-m_{V}$，可以简记为B−V。一般是短波段的星等减去长波段的星等。

恒星的光谱型和颜色有较好的对应关系，可以通过和已知类型的恒星的多个颜色的比较来归类新观测的恒星的光谱型。

恒星的颜色是个很重要的参量，测定恒星的光谱型非常费时，但得到恒星的颜色相对容易得多，特别是对于较暗的星。

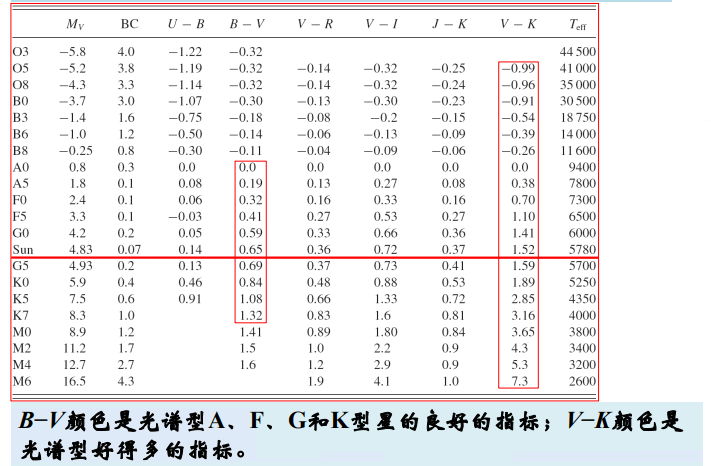
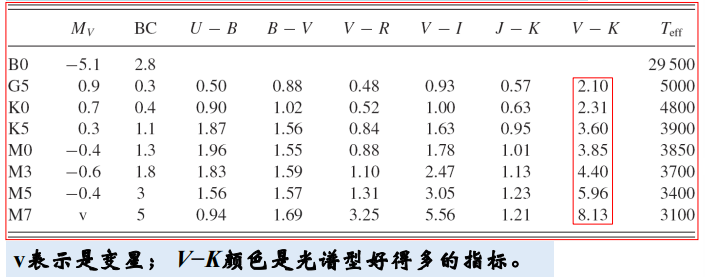
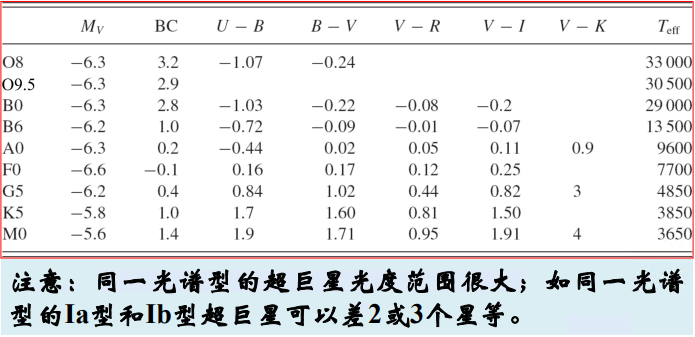
有效温度（effective temperature）$T_{eff}$

与某一恒星具有相同半径和相等总辐射能的绝对黑体的温度。

https://nadc.china-vo.org/astrodict/termdetails?id=8535

(1)恒星是炽热的致密气体球，其光谱近似于黑体谱。
(2)对于光度为L，半径为R的恒星，我们定义其有效温度$T_{eff}$：$T_{eff}$为相同半径，辐射相同总能量的黑体的温度。
(3)这个温度通常接近恒星“表面”的温度，即光球上气体温度的平均值。（光球是恒星的光能够逸入空间的那一层）

有效波长（effective wavelength）$\lambda_{eff}$

①滤光片：是用来选取所需辐射波段的光学器件。
②滤光片透过率曲线(滤光片带通)：它确定在波长λ透过的光的比例(0≤τ(λ)≤1)。若λ处的所有光都透过滤光片，则τ(λ)=1，而τ(λ)=0则表示在λ波长处没有光通过。由滤光片描述的天体在滤光片中(带通为τBP)的流量为：

\begin{equation}
F_{BP}\equiv\int_{0}^{\infty}\tau_{BP}(\lambda)F_{\lambda}(\lambda)\text{d}\lambda\approx F_{\lambda}(\lambda_{eff})\Delta\lambda
\end{equation}

其中$\lambda_{eff}$称为这个滤光片的有效波长，Δλ称为这个滤光片的带宽。

标准波长

标准波长的定义为：

\begin{equation}
\lambda_{0}=\frac{\int\lambda\tau(\lambda)\text{d}\lambda}{\int\tau(\lambda)\text{d}\lambda}
\end{equation}

带宽修正（bandpass corrections）

由于通过滤光片带宽的存在，使得测得的流量是整个天体的流量跟滤光片的相应函数卷积后的值。若两个天体通过滤光片测得的流量相同，但是其在标准波长上的流量就可能不同，反之同理。

因此，需要对流量做带宽修正，以得到在标准波长上的流量值。

若某天体在标准波长上的真实流量为$f(\lambda=\lambda_{0})$

其通过滤光片测得的流量为：

\begin{equation}
(\frac{\int\frac{f_{\lambda}\lambda}{hc}\tau_{\lambda}\text{d}\lambda}{\int \tau_{\lambda}\text{d}\lambda})h\frac{c}{\lambda_{0}}
\end{equation}

左边是通过滤光片得到的总光子数，右边是假定这些光子的波长为有效波长。

测得流量与真实流量之间的比值即为带宽修正。

带宽修正需要源的光谱形状来修正得到源在标准波长上的真实流量。

为了减少带宽修正，有时会用有效波长来代替标准波长。

\begin{equation}
\lambda_{eff}=\frac{\int \lambda^2\tau(\lambda)\text{d}\lambda}{\int \lambda\tau(\lambda)\text{d}\lambda}
\end{equation}

消光（extinction）$k,A$

天体辐射受到中介宇宙尘和地球大气的吸收与散射而造成的强度的减弱和颜色的变化。

https://nadc.china-vo.org/astrodict/termdetails?id=9157

消光可以分为星际消光和大气消光。

Extinction=Absorption+Scattering

可以写作：

\begin{equation}
\mu\frac{\text{d}I_{\lambda}}{\text{d}s}=-\kappa\rho I_{\lambda}+j_{\lambda}
\end{equation}

其中，$I_{\lambda}$代表着在$\lambda$波段方向$\text{arccos}\mu$向着空间坐标$s$的辐射强度。$\kappa$代表每单位质量密度为$\rho$的介质的消光系数，$j_{\lambda}$代表着发射系数。

有更简单的形式：

\begin{equation}
I_{\lambda}=I_{\lambda0}\text{exp}(-\int^{s}_{0})\kappa_{\lambda}\rho\text{d}s/\mu
\end{equation}

大气消光

大气消光的原因：

• 瑞利分子散射
• 水汽散射
• 尘埃散射
• 氧分子和水分子的吸收

大气消光可以写为：

\begin{equation}
f(\lambda,\xi )=f_{0}(\lambda)exp[-k(\lambda)X(\xi)]
\end{equation}

其中，$\xi$代表天顶距，$k(\lambda)$代表消光系数，$X(\xi)$代表大气质量

大气质量

当天顶距$\xi$小于45度时，大气质量可以写作：

\begin{equation}
X(\xi)=\text{sec}(\xi)
\end{equation}

当大于45度时，由于大气层的弯曲和折射，大气质量变为：

\begin{equation}
X(\xi)=\text{sec}[1-0.0012(\text{sec}^{2}(\xi)-1)]
\end{equation}

星际消光

星际消光的消光量：

\begin{equation}
A_{\lambda} \equiv-2.5\text{lg}(F_{\lambda}/F^{0}_{\lambda})
\end{equation}

$F_{\lambda}$是天体实测的流量，$F^{0}_{\lambda}$是未经消光的流量。

在其他资料中也写作：

\begin{equation}

A_{\lambda}=m_{\lambda,0}-m_{\lambda,real}
\end{equation}

$m_{\lambda,0}$大气外视星等

$m_{\lambda,real}$未受消光的真实星等

流量（flux）$F,f$

可以参考辐射流的定义

视亮度或流量是观测者的望远镜每秒每平方厘米接收到的能量，单位是尔格/厘米²/秒 ，用F表示

\begin{equation}
F=\frac{L}{4\pi d^{2}}
\end{equation}

其中，d为恒星距观测者的距离，L为恒星的光度，则F为测量到的流量。

光源的视亮度或流量与其距离的平方成反比，距离增加1倍，亮度便减为1/4。

一般不测量一颗恒星发射的全部波段内的流量，而只测量一个给定波长或频率间隔内发射光的流量，如下式：

\begin{equation}
F_{\lambda_{0}}=\int_{\lambda_{1}}^{\lambda_{2}}F_{\lambda}(\lambda)\text{d}\lambda
\end{equation}

梯度（gradient）$\Phi,G$

照度（illuminance，irradiance ）$f$

单位时间内投射到单位面积上的辐射能量。

https://nadc.china-vo.org/astrodict/termdetails?id=22560

星际红化（interstellar reddening）$E$

星际尘埃散射蓝光比红光利害，造成星光变红的现象。

https://nadc.china-vo.org/astrodict/termdetails?id=11402

线指数？（line index）

光度（luminosity ）$L$

天体表面单位时间辐射的总能量，即天体真正的发光能力。

https://nadc.china-vo.org/astrodict/termdetails?id=12175

光度是恒星每秒钟发出的能量，单位是瓦或每秒尔格，光度相当于功率，用L表示。

星等带宽？（magnitude bandwidth）

金属度指数？（metallicity index）$m_{1}$

①一般把重于氦的元素叫重元素或金属。

②重元素与氢和氦质量的百分比定义为金属丰度，用Z表示，如太阳的Z⊙≈0.02，即重元素只占百分之二，百分之九十八的是氢和氦。

\begin{equation}
\left [ A/B \right ] \equiv log_{10}\left \{ \frac{(N_{A}/N_{B})_{\star} }{(N_{A}/N_{B})_{\odot }}  \right \} 
\end{equation}

其中★和⊙分别代表恒星和太阳；A和B代表两种元素名称，NA和NB指这两种元素的原子个数。例如某一天体：[Fe/H]=−2，说明这个天体中铁原子个数和氢原子个数的比是太阳中铁原子个数和氢原子个数比的百分之一，即这个天体的金属丰度为−2。

单色星等？（monochromatic magnitude）$m_{\lambda}$

谱分辨率（spectral resolution）

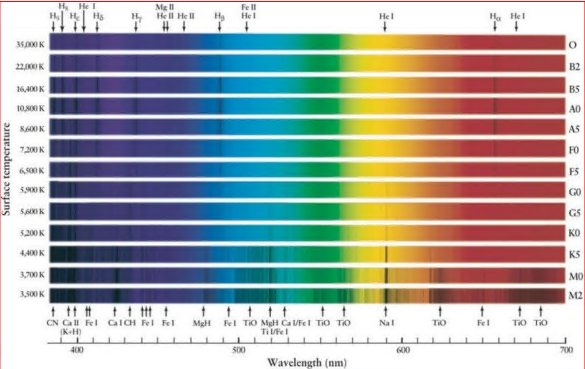
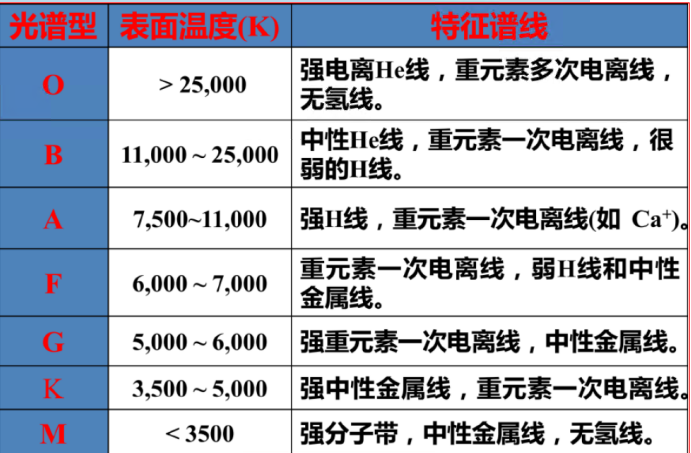
光谱型（spectral type）

正常的恒星光谱

由连续光谱和其上叠加的吸收线组成。恒星的光谱由恒星的有效温度、表面重力加速度(影响谱线的宽度)以及恒星中各种化学元素的多少(化学丰度)共同决定。

目前常用的恒星光谱分类法把恒星的光谱分为7类或10类：
O－B－A－F－G(－R－N)－K(－S)－M

每一类又有10个小类，用0−9表示，是恒星表面温度的序列，表示温度越来越低。一般把具有O－B－A光谱的恒星定义为早型星，其余的为晚型星。

标准星（standard star）

在测光、光谱分类等天体物理观测中用作基准的恒星。

https://nadc.china-vo.org/astrodict/termdetails?id=17766

UBVRI系统：AJ 104(1992)339

uvby系统：A&A Suppl 11(1973)119

本文中的英文名词的中文翻译来自天文学名词（部分词汇天文学名词中无对应词条）

部分解释来自于国台马骏老师《星系天文学》课件

参考文献：

[1].Budding E, Demircan O. Introduction to astronomical photometry[M]. Cambridge University Press, 2007.

[2].王钰溪, 高健, 姜碧沩, 等. 银河系和河外星系的消光规律及尘埃性质[J]. 天文学进展, 2018, 36(3): 283-305.

[3].黄博闻等.大视场测光巡天流量定标方法