Bounce[2017 ACM 北京站网络赛]
题目7 : Bounce
描述
For Argo, it is very interesting watching a circle bouncing in a rectangle.
As shown in the figure below, the rectangle is divided into N×M grids, and the circle fits exactly one grid.
The bouncing rule is simple:
1. The circle always starts from the left upper corner and moves towards lower right.
2. If the circle touches any edge of the rectangle, it will bounce.
3. If the circle reaches any corner of the rectangle after starting, it will stop there.
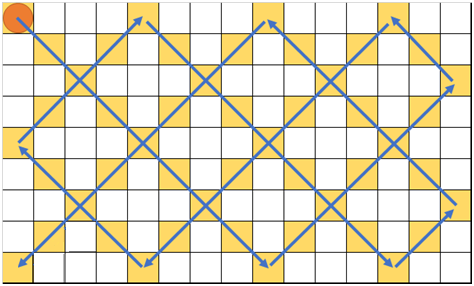
Argo wants to know how many grids the circle will go through only once until it first reaches another corner. Can you help him?
输入
The input consists of multiple test cases. (Up to 105)
For each test case:
One line contains two integers N and M, indicating the number of rows and columns of the rectangle. (2 ≤ N, M ≤ 109)
输出
For each test case, output one line containing one integer, the number of grids that the circle will go through exactly once until it stops (the starting grid and the ending grid also count).
- 样例输入
-
2 2 2 3 3 4 3 5 4 5 4 6 4 7 5 6 5 7 9 15
- 样例输出
-
2 3 5 5 7 8 7 9 11 39
这道题光找规律找了三个小时,找出来规律之后才发现题目原来很简单。
先算出来小球一共会经过多少网格(包括重复的在内)
再算出来有多少个网格过不止一次,两者相减就可以了。
对于n*m的矩形,经过观察可以得到,小球弹跳中经过的网格总数是$\frac{(n-1)\times (m-1)}{gcd((n-1),(m-1))}+1$.
可以算得 球在9*15的方格中会经过57个网格
然后又经过观察可以看出来,其实9*15的矩形(图中示意)和5*8的矩形是相似的,即5*8扩大一倍可以得到9*15的矩形。

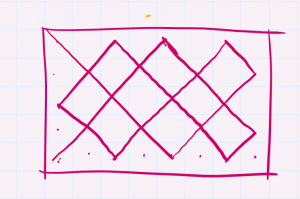
左边是9*15的网格 右边是5*8的网格。
这两个网格中的相交点都是一样的,都是9个,而(5-2)*(8-2)正好等于9*2!
而57-9*2就是答案39.
又是经过观察,显然可以得到一个结论:交点数等于 (n-2)*(m-2)/gcd(n,m)
而只经过一次的点就是57-9*2=39.
这样我们就得到了总的公式
$$f(x)=\frac{(n-1)\times (m-1)}{gcd((n-1),(m-1))}-(\frac{(n-1)}{gcd((n-1),(m-1))}-1)\times (\frac{(m-1)}{gcd((n-1),(m-1))}-1)+1$$
#include<bits/stdc++.h>
using namespace std;
long long gcd(long long a, long long b) {
while(b != 0) {
long long r = b;
b = a % b;
a = r;
}
return a;
}
int main() {
ios::sync_with_stdio(0);
long long n, m;
while(cin >> n >> m) {
if(n == m) {
cout << n << endl;
continue;
} else if(n > m) {
swap(n, m);
}
long long g = gcd(n - 1, m - 1);
long long gg = ((n - 1) / g) * (m - 1);
long long ggg = gg / (n - 1);
long long nn = (n - 1) / g;
long long mm = (m - 1) / g;
cout << gg - (nn - 1)*(mm - 1) + 1 << endl;
}
}

